Just as a recap, the u-tube video shows a vehicle that has a propeller that is geared to its wheels. It also has a wind streamer to indicate the apparent wind on the car. It is shown traveling downwind apparently faster than the wind. In the video, you can clearly see the apparent wind shift from behind the car to coming from in front of the car.
Here is the link to the video:
http://www.youtube.com/watch?v=aJpdWHFqHm0
Another video, showing a similar car going UP a treadmill is:
http://www.youtube.com/watch?v=MfZt19F-OA4&watch_response
And the discussion is all around if this is possible or is it a hoax.
I urge you to NOT bother reading the comments on the u-tube – mostly uninformed or mis-stated physics.
This is all about DWFTTW – Down Wind Faster Than The Wind.
First off, I can’t tell if the video is a hoax or not. There might be a fishing line pulling it. I can say this – the physics allows this to NOT BE A HOAX (so it probably isn’t).
Whenever we are sailing anything – sail boats, kites, paragliders, hang gliders, etc – we are pitting two forces against each other. In sailboats, it is the force of the wind on the sail against the force of the keel on the water. In Hang Gliding, it is the force of the wind (apparent wind) on the wing against gravity. In kites, it is the force of the string against the force of the wind on the kite.
People who are not sailors often cannot believe that a sailboat can sail partially upwind, but it can, and we do it all the time. This is sort of like wuffos that ask how we can fly hang gliders/paragliders into the wind.
Well we do sail partially into the wind –not directly upwind, but at an angle into the wind. This direction of sail (point of sail) is called a “close reach”. In order to proceed directly into the wind, you first sail on a close reach on a port tack (the wind from the left-front of the boat), then a close reach on a starboard tack (the wind from the right-front of the boat). You go back and forth between the two angles, and the net result is that you end up directly upwind.
How does this work? The keel resists all movement perpendicular to the length of the boat, and allows with little resistance movement in the direction of the boat. The force on the keel is always essentially perpendicular to the boat, and the strength of this force is whatever it takes to keep the boat from moving sideways. The force on the sail is always perpendicular the local sail. Now the sail is curved, but the overall force is the average of the entire sail. If the sail is off to the left of center, then the force of the sail will be forward and to the left. This is assuming the apparent wind is hitting the right side of the sail – if it isn’t, the sail is on the wrong side – you better duck!
Since the keel force is directly opposite and equal in magnitude to the part of the sail force that is pushing the boat to the left, the sum of the keel and sail force is directly forward.
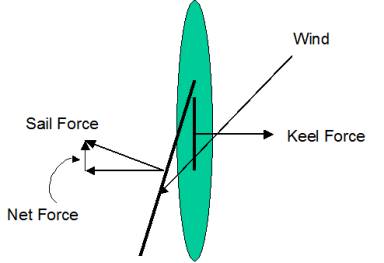
Now about down wind. It is well known in sailing that you cannot go directly downwind faster than the wind. This is called being on a “dead run”. You clearly CAN have your downwind component faster than the wind when you are going partially downwind. This is called a “broad reach”.
As you go faster and faster on the broad reach, the “apparent wind” shifts and seems to come from the front on the boat. This apparent wind is the vector sum of the actual wind and the wind induced by the velocity vector of the boat (directly from the front). Sailboat people talk about the boat being so good “it generates it’s own wind”, which is pure hogwash. It is still the true wind that is generating the power for the boat. The induced wind from the boat motion is directly in line with the boat, and cannot be used to push the boat forward – this would be like sailing directly into the wind. Here is the drawing:
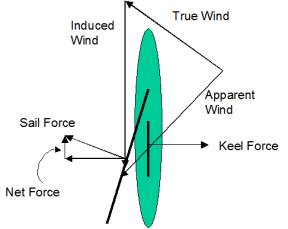
So if you double the size of the sails (in square dimensions), you double all of the forces, the boat goes faster. It can (and does) exceed the velocity of the wind.
Now if you have followed all of that, lets get on the device in the video. Here the force of the wheels on the ground is pitted against the force of the wind (apparent) on the blades. Remember that the wheels are geared to the blades, so the blades turn when the car moves.
When starting at rest, the apparent wind and true wind are the same, and this wind pushes the car forward downwind. The forward speed of the car then causes the blades to turn. No surprises for anyone there – right?
Now as the car reaches the speed of the wind: The apparent wind on the car is now NULL, and this caused to some folks to say that the car cannot do this, let alone go any faster. What they have overlooked is that it is not the “apparent wind” in the reference of the car that counts here, it is the “apparent wind” in the reference of the MOVING blade. Because of the pitch of the blade and the speed of the blade, the “apparent wind” at the blade is still hitting the BACK side of the blade, and this is what pushes the car forward.
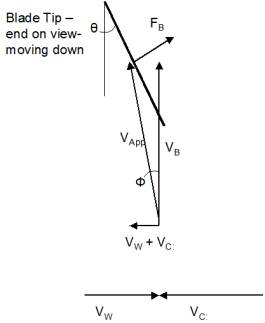
Here is a drawing, showing the blade tip as viewed end-on. In this drawing, the blade tip is moving down, and the car is moving to the right:
And the math:
Assuming the blades only exist at the tip of the propeller arm, and that the cart has no drag or losses:
Define
θ: the angle of the Blade tip relative to vertical
G: the ratio of the speed of the wheels to the blade tip speed (the gearing ratio)
Ф: the angle of the apparent wind at the tip (relative to vertical)
VApp: apparent wind at the blade (vector)
VB: wind induced by blade rotation (vector)
VW: true wind vector
VC: wind induced by the motion of the car
SC: the speed of the car = ||VC ||
SB: the speed of the blade = ||VB ||
SApp: the apparent wind speed at the blade = ||VApp
||
SW: the true speed of the wind = ||VW ||
A: the Area of the blade tip
δ: the density of the air
c: an aerodynamic constant
Then
SC = SB*G
tan(Ф) = (SC-SW) / SB
tan(Ф) = (SC-SW) / (SC/G)
note that Ф=0 as the car reaches the speed of the wind
The apparent wind vector in the frame of the blade tip (and the drawing) is the vector sum of the true wind, the induced wind from the car motion, and the induced wind from the blade rotation. The first two are collinear that opposite, while
the blade motion is perpendicular to the line of motion of the car/wind.
VApp = VB + VW + VC (all vectors)
SApp= ||VApp|| = ||VB + VW + VC || = sqrt(||VB||2 + ||VW + VC ||2 ) = sqrt( SB2 + (SW - SC ) 2 )
SApp2 = SB2 + (SW - SC ) 2
The force on the blade is:
FB = Aδc * sin(θ- Ф) * SApp2
FB = Aδc * sin(θ- Ф) * (SB2
+ (SW -SC)2)
FB = Aδc * sin(θ- Ф) * (SC2
/G2 + (SW -SC)2)
The component of the force going forward is:
FBF = FB *cos(θ)
FBF = Aδc * sin(θ- Ф) * (SC2 /G2 + (SW -SC)2) *cos(θ)
And the component resisting the turning of the blade is:
FBU = FB *sin(θ)
FBU = Aδc * sin(θ- Ф) * (SC2 /G2 + (SW -SC)2) *sin(θ)
Because of the gearing, the force on the wheels resisting the forward motion is:
FW = FBU / G
FW = Aδc * sin(θ- Ф) * (SC2 /G2 + (SW -SC)2) *sin(θ) /G
The total force is:
FT = FBF
- FW
FT = Aδc * sin(θ- Ф) * (SC2 /G2 + (SW -SC)2)
*cos(θ) - Aδc * sin(θ- Ф) * (SC2
/G2 + (SW -SC)2) *sin (θ) /G
FT = Aδc * sin(θ- Ф) * (SC2
/G2 + (SW -SC)2)
* (cos(θ) - sin (θ)/G)
FT = Aδc * sin(θ- Ф) * (SC2
/G2 + (SW -SC)2)
* sin (θ) * (1/tan(θ) - 1/G)
So the direction of the force depends on the term (1/tan(θ) - 1/G)
Now consider for a moment what would happen if the slope of the blade and the Gearing ratio where essentially the same (tan(θ) = G)
Then the total force is zero– and the car will not go anywhere.
But if the blade angle is decreased, or the Gearing ratio G is increased, then tan(θ) < G and (1/tan(θ) - 1/G) is positive. The force will therefore be positive, and the car will accelerate forward.
The forward force exceeds the backward force and the car accelerates. This continues until, in the idealized case, Ф approaches θ and both forces go to zero. In the real case, as Ф gets closer to θ, the forces get smaller, and the drag/loss forces stop the acceleration.
Note that Ф approaches θ only at car speeds greater than the wind speed.
If the car can be built with sufficiently low drag/loss characteristics, it can thus go faster down wind than the wind.
As one simplified example, consider the car moving at exactly the speed of the wind.
At this speed Ф=0, and
FT(SC=SW) = Aδc * sin(θ) * (SC2
/G2 * sin (θ) * (1/tan(θ) - 1/G)
FT(SC=SW) = Aδc * sin2(θ) * SC2 /G2 * (1/tan(θ) - 1/G)
So when the car is moving at the speed of the wind, the forward force is still positive, as long as the blade angle is less than the Gearing ratio G. So the car accelerates faster than the speed of the wind.
Now as a double-check, what does the equation say about the behavior in no wind – the car better not be moving!
With no wind:
tan(Ф) = (SC-SW) / (SC/G)
tan(Ф) = (SC-0) / (SC/G)
tan(Ф) =G
Well we already know that tan(θ) < G for our car to work, so tan(Ф) > tan(θ), and Ф > θ.
Thus, if the car is moving, the wind is blowing on the wrong side of the blade. The force is;
FT = Aδc * sin(θ- Ф) * (SC2 /G2 + (SW -SC)2) * sin (θ) * (1/tan(θ) - 1/G)
but sin(θ- Ф) is negative, so the car will be decelerating to a stop.
(If the wind is zero and the car is not moving, Ф is undefined – duh!)
If you made it to here, we should start a club. People like us need friends too.
(version 2 – 11/13/2008)